재귀 함수를 만들어서 사용하는 문제들로 구성되었습니다.
재귀 함수의 핵심은 정의된 함수 1개가 연속해서 호출되고,
결괏값까지 도출할 수 있어야 한다는 것입니다.
제공된 문제의 내용이 너무 어렵지 않아서 연습하기 좋았습니다.
문제 9.
1~n까지의 합 재귀 함수
int resum(int n); //함수 정의
//main()
printf("1~20까지의 합 = %d", resum(20));
//재귀 합
int resum(int n){
if(n==1) return 1;
return n + resum(n-1);
}
1~n까지의 합을 구하는 재귀 함수는 int형 인자 1개를 받아옵니다.
int형 인자는 n의 값에 해당하며 코드에서는 n = 20으로 하였습니다.
재귀 함수 구성에서 중요한 것은 끝맺음할 수 있는 값이 있어야 한다는 것입니다.
끝맺음을 할 수 없다면 재귀 함수는 무한루프에 들어가 강제 종료 없이는 멈출 수 없을 것입니다.
재귀 함수 resum()의 진행 구성은 다음과 같습니다.
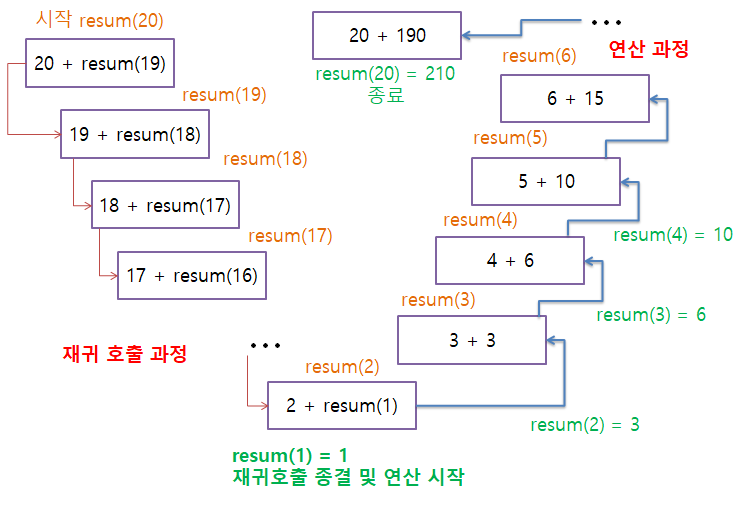
재귀 호출이 발생하게 되면 함수의 연산은 이루어지지 않습니다.
더 이상의 호출이 발생하지 않을 때까지 재귀 호출은 계속되며
마지막 호출 후 끝맺음을 의미하는 값이 반환되면 연산이 시작됩니다.
연산은 호출이 된 순서의 역순으로 진행되기 때문에
마지막 연산은 처음 호출된 resum(20)에서 이루어집니다.
문제 10.
피보나치 수 구하기
int fibo(int n);
//main()
int count = 10;
for(int i=0; i<11; i++){
printf("%d ", fibo(i));
}
//피보나치 수
int fibo(int n) {
if (n==0) return 0; //fibo(0) = 0
else if (n==1) return 1; //fibo(1) = 1
else return fibo(n-1) + fibo(n-2);
}

피보나치 수는 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... 의 값을 가집니다.
n번째 수는 n-1, n-2번째 수의 합과 같으며
1번째, 2번째 수는 0, 1로 고정되어 있습니다.
따라서 재귀 함수를 만들 때 끝맺음을 할 수 있는 값은 0과 1로 2개 지정합니다.
피보나치 수를 만드는 함수는 인자로 n번째의 n을 받아옵니다.
코드에서는 10을 받아왔기 때문에 10번째 값까지 출력합니다.
재귀 함수 호출 및 연산 방식은 위의 그림을 참고해서 생각해보시면 됩니다.
문제 11.
x의 y승 재귀 함수
double Make_pow(int baseN, int countN); //x의 y승 계산
int count = 10; //10승까지 만들기
int base = 6; //밑수
for(int i=0; i<count+1; i++){
printf("%d의 %d승은 = %.lf\n",base, i, Make_pow(6, i));
}
//x의 y승 계산
double Make_pow(int baseN, int countN){
if(countN==0) return 1;
return baseN * Make_pow(baseN, countN-1);
}

x의 y승 계산 재귀 함수 Make_pow()는 인자로 밑수(baseN)와 지수(countN)를 받아옵니다.
문제에서 밑수는 6으로 지정했기 때문에 baseN의 값은 6으로 일정합니다.
countN의 경우는 6을 곱하는 횟수를 의미하기 때문에
0인 경우에는 6의 0승 = 1의 값을 가집니다.
따라서 끝맺음은 countN=0일 때 1의 값을 반환합니다.
간단하게 문제 9번의 1~n까지의 합의 재귀 함수에서
+ 연산이 * 연산으로 바뀌었다고 생각하시면 됩니다.
문제 12.
재귀 함수로 16진수 만들기
void Hex(int n);
int num; //입력받을 정수
scanf_s("%d", &num, sizeof(int));
printf("입력된 값 = %d\n", num);
Hex(num);
//16진수 변환
void Hex(int n){
if(n>16) {
Hex(n/16);
printf("%.X",n%16); //나머지 출력
}
//끝맺음 값 출력
else printf("%.X",n);
}

10진수인 정수형 값을 16진수로 변환하는 재귀 함수 Hex()를 만들었습니다.
인자는 16진수로 변환할 정수형 값을 받아옵니다.
10진수를 16진수로 변환하는 방식은 아래의 그림과 같습니다.

10진수를 더 이상 16으로 나눌 수 없을 때까지 나누기 연산을 하고 결과를 몫과 나머지의 조합으로 표현합니다. 함수 자체에서 값을 출력할 수 있도록 하였습니다.
10진수가 16보다 클 경우 재귀 호출을 하여 16으로 나눈 몫을 다시 나누기합니다.
더 이상 나눌 수 없다는 것은 16보다 작다는 뜻이기 때문에
else를 통해 그 값을 16진수로 뽑아냅니다.
값을 출력했다는 것은 끝맺음이 발생했다는 것과 같은 의미이기 때문에
재귀 호출이 끝나고 최종적으로 다음 연산이 진행됩니다.
-끝-
'작업 > Programming' 카테고리의 다른 글
| C언어 특정 문자를 기준으로 문자열을 나누고 역순으로 출력 (0) | 2020.06.11 |
|---|---|
| C언어 문자열 역순으로 출력 (0) | 2020.06.11 |
| Perfect C 프로그래밍 연습 10장 1, 3, 4, 5번 해결 (0) | 2020.06.09 |
| C언어 행렬의 곱 구하기 (0) | 2020.06.05 |
| Perfect C 프로그래밍 연습 9장 7, 8, 9, 10번 해결 (0) | 2020.06.04 |




