
동적 계획법 (Dynamic Programming)
- 하나의 큰 문제를 중복(반복)된 하위 문제들로 분해하여 계산한다.
- 하위 문제들의 계산 결과를 저장 후, 상위 문제의 계산에 재사용한다.
- 하위 문제들의 결과를 저장하는 테이블을 사용하며 메모리 사용량이 증가할 수 있다.
Memoization기법을 사용한다.- 반복문이나 재귀를 통해 구현할 수 있다.
배낭 문제 (Knapsack Problem)
- 동적 계획법 알고리즘의 이해를 돕는 기본 문제.
- 물건을 W 무게까지 담을 수 있는 배낭이 있고, N개 종류의 물건들이 각각 무게(g)와 가치(v)를 가지고 있다.
- W 무게를 넘지 않으며 '최대 가치'가 될 수 있도록 물건을 배낭에 담는 방법을 찾아낸다.
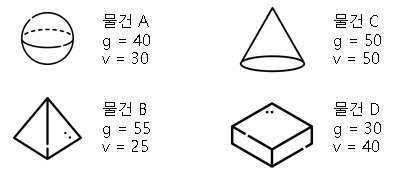
물건을 조합할 수 있는 경우를 구해보면 아래 그림과 같다.
3개 조합부터는 무조건 무게 100을 넘기 때문에 2개 조합만 계산했다.
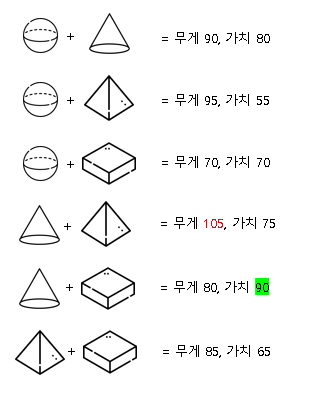
배낭에 담을 수 있는 총 무게 100을 넘지 않으면서 최대의 가치를 계산했을 때,
90이 가장 높은 가치임을 확인했다.
이제 문제 해결을 위한 계산 과정을 Memoization Table을 사용해 진행한다.
Memoization
- 상위 문제 : 배낭의 무게를 초과하지 않으면서 가장 높은 가치를 가질 수 있는 물건 조합 찾기.
- 하위 문제 : 물건을 배낭에 담을 수 있을 때 계산된 최대 가치.
- 상위 문제를 해결하기 위해 하위 문제에 대한 계산 결과를 테이블에 저장하며 재사용한다.
- 반복문이나 재귀를 사용하여 테이블 내의 데이터를 채워나간다.
2차원(행렬) 데이터에서 행(Row)의 값은 배낭에 담을 수 있는 물건들에 해당한다.
열(Column)의 값은 배낭에 담을 수 있는 허용 무게에 해당한다.
계산 알고리즘을 구현하기 위해서는 초깃값(0) 행과 열이 필요하다.
그래서 무게와 가치가 모두 0인 물건의 행과 배낭의 무게가 0인 열을 테이블에 추가한다.
결국 테이블의 2행 2열부터 배낭에 담을 수 있는 물건과 그때의 가치를 계산하며 테이블을 채우게 된다.
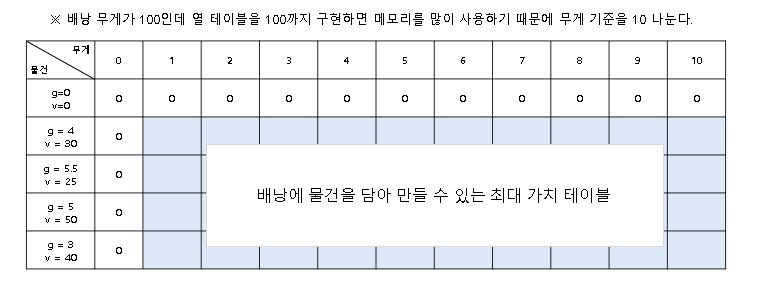
배낭 문제의 해결 과정은 다음과 같다. 글로만 적혀있어 이해가 어렵다면 그림으로 표현한 과정을 보고 나서 다시 읽어본다.
① 해당 무게(열)에서 물건(행)을 담을 수 있는지 검사한다.
② 물건을 담을 수 있다면, 해당 물건(행)을 담기 전의 최대 가치에 물건을 담고 나서의 가치를 더한다.
③ ② 과정에서 계산된 가치와 해당 무게(열)에서 가장 높게 계산된 가치를 비교한다.
④ ③ 과정에서 가장 높게 계산된 가치를 테이블의 값으로 추가한다.
⑤ 마지막 값까지 계산되도록 ①~ ④ 과정을 반복한다.
메모이제이션 테이블은 '허용된 배낭의 무게에서 가질 수 있는 최대 가치'를 계산한 결과를 저장한다.
즉, 2행 2열은 '물건A(2행)가 무게 1인 배낭(2열)에 들어갈 수 있나 없나를 검사 후, 그때의 최대 가치'를 저장한다.
무게가 100(테이블에서는 10을 나누었으므로 10)인 배낭에 담을 수 있는 최대 가치는 5행 11열인 가장 우측 하단 값이 된다.
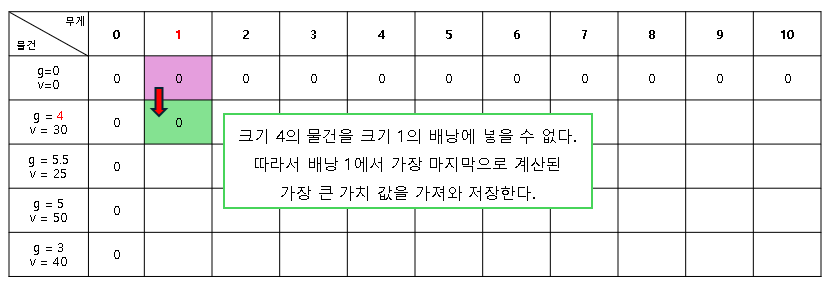
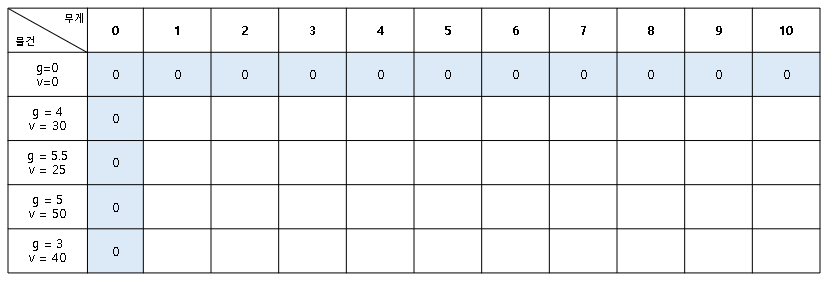
해당 위치(초록 셀)에서 배낭에 물건을 담을 수 있는지 검사한다.
위의 경우, 물건의 무게가 배낭의 허용 무게를 초과하였으므로 담을 수 없다.
그러면 해당 배낭의 무게에서 가장 큰 가치를 가져와 저장하는데 이는 이전 행의 열 값에 해당한다.
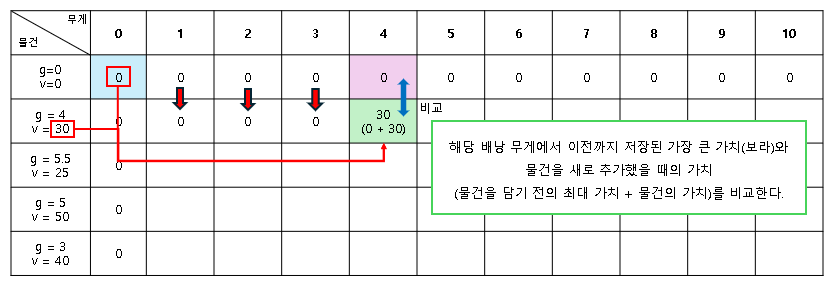
물건을 배낭에 담을 수 있는 상태면 다음 순서로 진행한다.
① 물건을 배낭에 담기 전의 배낭 가치를 저장한 값을 가져온다.
- 무게 4의 배낭에 무게 4의 물건을 넣기 전에는 무게 0(4-4)의 배낭 가치와 같았을 것이다.
- 따라서 이전 행의 무게 0인 배낭의 가치(파란 셀) 값을 가져온다.
② 배낭에 물건을 새로 추가했을 때의 가치를 계산한다.
- 무게 0일 때의 배낭 가치(파란 셀) + 무게 4인 물건의 가치(30) = 0+30 = 30
③ 해당 무게의 배낭이 가지고 있던 최대 가치(보라 셀)와 새로 계산된 가치(30)를 비교한다.
- 같은 열을 기준으로 이전 행의 값이 물건을 추가하기 전 가장 높게 계산된 가치에 해당한다.
- 물건을 추가하기 전, 0이 최대 가치였던 무게 4의 배낭은 무게 4의 물건을 추가하게 되면서 30으로 가치가 높아졌다.
④ 가장 높은 값을 추가(저장)한다.
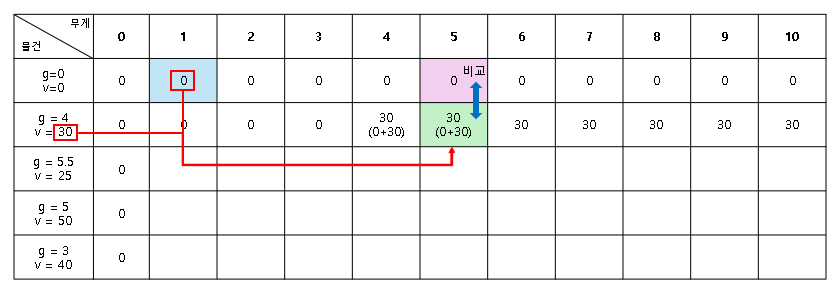
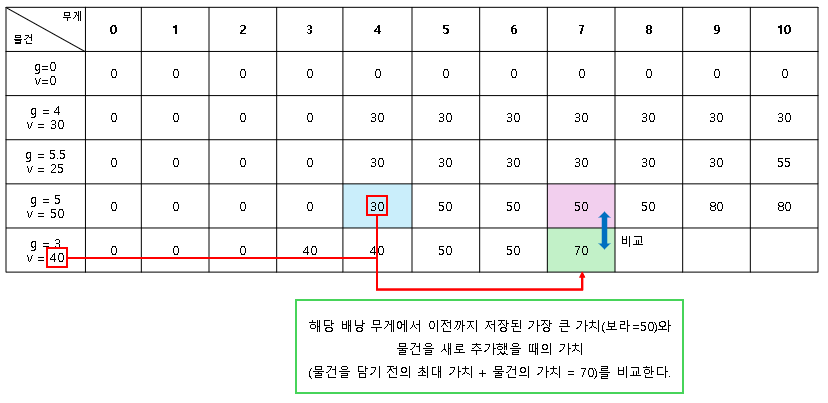
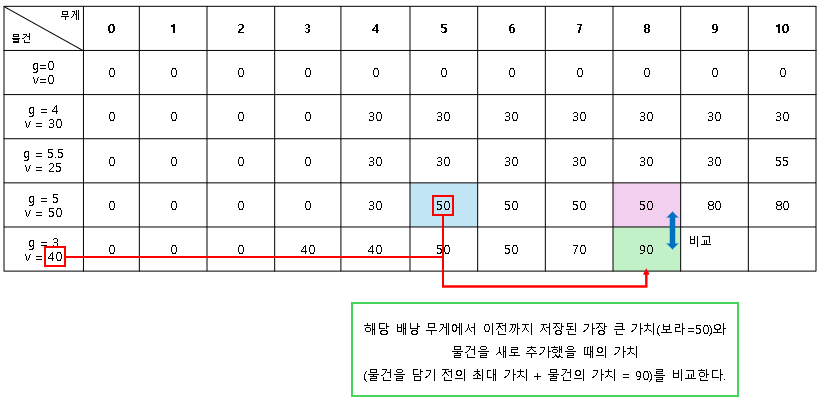
다른 빈 셀도 물건을 담을 수 있을 때, 동일한 방법으로 데이터를 비교하며 채워 나간다.
(해당 배낭 크기(열)에서 가장 큰 가치 - 보라 셀) vs (물건을 담기 전 배낭의 가장 큰 가치 - 파란 셀) + 추가할 물건의 가치
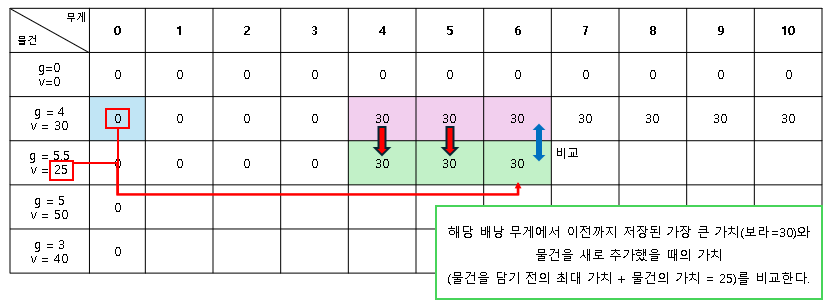

2행을 기준으로 배낭 10에서는 이전까지의 기록 상 30이 가장 큰 가치였다.
3행을 진행하면서 물건을 추가할 수 있음을 확인했고,
5.5 무게의 물건을 담기 전 10-5.5=4.5 수준의 배낭에서 무게 4인 물건을 담은 30 가치의 배낭이 가장 높은 값이었다.
거기에 5.5 무게의 물건을 추가하니 30+25=55가 되었고, 이는 이전 배낭 10의 30가치보다 높다.
따라서 55로 업데이트한다.
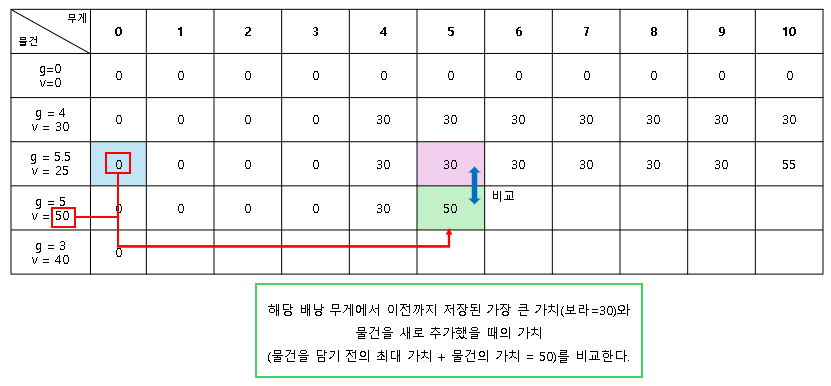
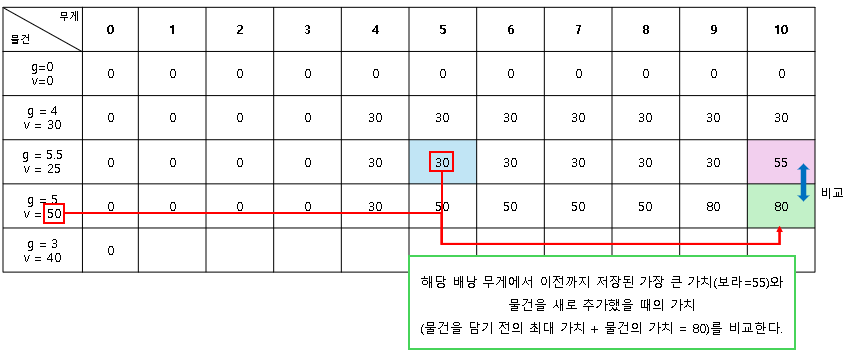
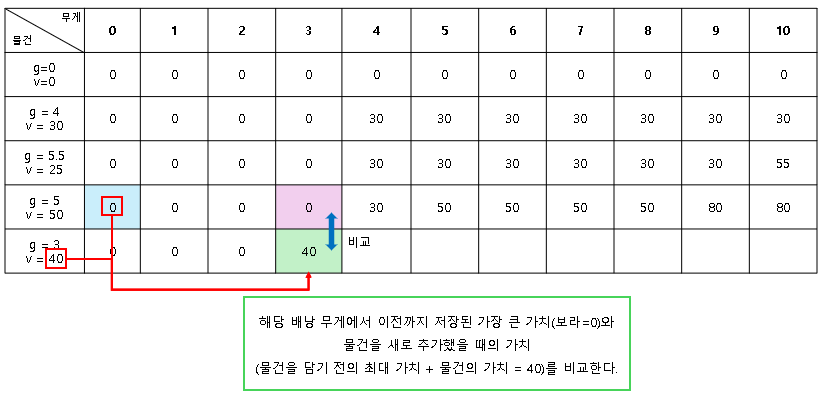
배낭 문제 해결에 도달한 메모이제이션 테이블은 다음과 같다.
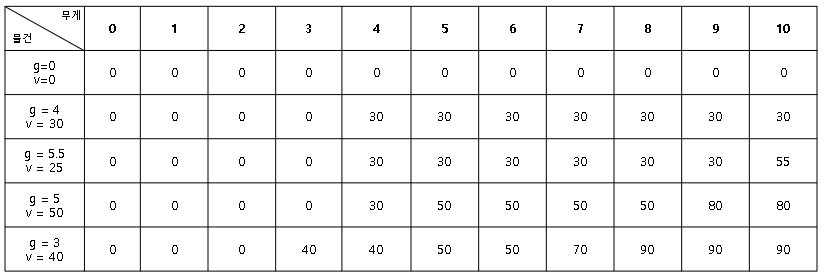
가장 우측 하단의 90이 배낭 무게 100(테이블에서는 10나눈 값인 10)을 초과하지 않고 물건을 담았을 때 가장 높은 가치다.
---
이번에는 위에서 진행한 배낭 문제를 Python 코드로 구현하고 메모이제이션 테이블을 확인해 본다.
먼저 배낭의 허용 무게와 물건들의 무게와 가치를 정의한다.
ob = ([40,30], [55,25], [50,50], [30,40]) # [무게, 가치]
knap = 100 # 배낭 무게
메모이제이션 테이블로 배낭의 무게 0~100까지의 열을 구성해야 하는데 이는 메모리를 많이 사용한다.
따라서 10을 나눈 값을 사용해 테이블을 구성하고 무게를 계산하도록 한다.
배낭 무게는 정수 단위로 변환하지만,
물건의 무게는 55값이 실수 5.5로 만들어지므로 float를 유지한다.
# Memoization Table 크기 단축을 위해 무게를 10 나눔
knap = int(knap / 10)
ob = [(division_10(w), v) for w,v in ob]
# print(ob)
# [(4.0, 30), (5.5, 25), (5.0, 50), (3.0, 40)]
메모이제이션 테이블에서 각 행은 물건을 담는 여부에 따라 값을 업데이트할 목적으로 사용되며
각 열은 배낭의 무게 0~10까지의 경우에 해당한다.
이때, '이전값 비교' 조건을 사용하여 가치를 계산하기 때문에 초깃값으로 1행과 1열을 0의 물건과 0의 배낭으로 추가한다.
행 개수 = 물건 4개 + 초깃값 물건(0) 1개 = 5개
열 개수 = 배낭 무게 0~10 = 11개
# Memoization Table
memotable = [[0 for _ in range(knap+1)] for _ in range(len(ob)+1)]
2차원 구조의 데이터이므로 반복문을 사용 시 중첩 for문 구조가 된다.
슈도 코드(pseudo code)는 다음과 같다.
for 행 단위 탐색:
# 첫 번째 열(0번 인덱스)은 배낭의 무게 0이므로 어떤 물건도 담을 수 없음 = 초깃값 0
for 열 단위 탐색(1, 배낭무게+1):
if 배낭에 담을 수 없는 물건인가? :
배낭의 가장 높은 가치를 가져와 메모이제이션 테이블에 저장.
elif 배낭에 담을 수 있는 물건인가? :
max( (배낭에 물건을 담기 전 배낭의 최대 가치 + 물건의 가치),
(현재 무게의 배낭의 최대 가치) )
max의 결과를 메모이제이션 테이블에 저장.
# 1행은 초깃값(0)을 배치하는 구간.
for row in range(0, len(ob)):
# 1열은 배낭의 허용 무게가 0이므로 초깃값(0)과 같다.
for col in range(1, knap+1):
if ob[row][0] > col: # 배낭에 담을 수 없는 무게면
memotable[row+1][col] = memotable[row][col] # 해당 배낭 무게의 최대 가치를 가져옴
elif ob[row][0] <= col: # 배낭에 담을 수 있는 무게면
tmp = max(memotable[row][col],
ob[row][1] + memotable[row][col-int(math.ceil(ob[row][0]))])
memotable[row+1][col] = tmp
for i in range(len(memotable)):
print(memotable[i])

'작업 > Programming' 카테고리의 다른 글
| IntelliJ SpringBoot 서버 실행 후 즉시 종료 문제 (1) | 2024.10.06 |
|---|---|
| 파이썬(Python) 진법(2, 8, 16) 변환 (0) | 2021.08.22 |
| 파이썬(Python) abs, all, any 함수 (0) | 2021.08.22 |
| 파이썬(Python) zip 함수 사용 (0) | 2021.08.15 |
| 파이썬(Python) 폴더 및 파일 이름 바꾸기 (2) | 2021.08.13 |




