
문제
1보다 큰 자연수 중에서 1과 자기 자신을 제외한 약수가 없는 자연수를 소수라고 한다.
예를 들어, 5는 1과 5를 제외한 약수가 없기 때문에 소수이다.
하지만, 6은 6 = 2 × 3 이기 때문에 소수가 아니다.
골드바흐의 추측은 유명한 정수론의 미해결 문제로,
2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다는 것이다.
이러한 수를 골드바흐 수라고 한다.
또, 짝수를 두 소수의 합으로 나타내는 표현을 그 수의 골드바흐 파티션이라고 한다.
예를 들면, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5, 12 = 5 + 7, 14 = 3 + 11, 14 = 7 + 7이다.
10000보다 작거나 같은 모든 짝수 n에 대한 골드바흐 파티션은 존재한다.
2보다 큰 짝수 n이 주어졌을 때, n의 골드바흐 파티션을 출력하는 프로그램을 작성하시오.
만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력한다.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다.
각 테스트 케이스는 한 줄로 이루어져 있고 짝수 n이 주어진다. (4 ≤ n ≤ 10,000)
출력
각 테스트 케이스에 대해서 주어진 n의 골드바흐 파티션을 출력한다.
출력하는 소수는 작은 것부터 먼저 출력하며, 공백으로 구분한다.

문제에서 제시된 입력의 최대 범위인 10000의 두 소수를 구해보았으며 4919, 5081 두 값이 나왔습니다.
값을 구하는 과정을 함수로 만들어서 적용하였으며 곧 답이 되었습니다.
구현하기 위해서 먼저 소수들을 저장한 리스트를 만들었습니다. (prime_number 리스트)
소수를 찾아내는 범위는 2에서 6000으로 지정했는데 그 이유는 답을 도출하는 방법과 연관되어 있습니다.
값 도출 방법
문제에서 주어진 예시 중 "4 = 2 + 2, 12 = 5 + 7"에서 힌트를 얻었습니다.
짝수를 2로 나누었을 때 그 값이 소수이면 그 수를 더하면 됩니다.
만약 나누었을 때 소수가 등장하지 않는다면 그 값을 중앙값으로 크고 작은 소수를 찾습니다.
12를 예시로 2를 나눈 값인 6은 소수가 아닙니다.
6을 기준으로 큰 소수는 7이며 작은 소수는 5입니다. 이 둘을 더하면 12가 나옵니다.

12의 경우와 같이 큰 수와 작은 수로 소수가 바로 등장한다면 좋겠지만 큰 수일수록 그 경우는 적습니다.
그래서 소수를 빨리 찾으려는 방법으로 미리 소수들을 저장한 리스트를 만든 다음,
"짝수 / 2"의 값을 기준으로 크고 작은 소수를 찾아내는 방법을 사용하였습니다.
''' 구할 수 있는 최댓값인 10000의 경우에는 division 2를 했을 시에 5000이 나옵니다.
그리고 직접 구했을 때 4919와 5081의 조합으로 10000을 얻을 수 있었습니다.
그래서 넉넉히 6000까지의 값 중에서 소수를 찾아내어 리스트에 저장하였습니다. '''
다음으로, 처음으로 알아낸 두 소수의 합이 원하는 값이 아닐 경우입니다.
10000을 예시로 진행하겠습니다.
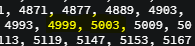
5000을 기준으로 두면 크고 작은 소수는 4999와 5003이 나옵니다. 하지만 둘의 합은 10002입니다.
문제에서 요구한 "두 소수의 차이가 가장 작은 것을 출력"을 만족하기 위해서 규칙을 정했습니다.
① 두 소수의 합이 정답보다 클 경우 -> 더 작은 소수로 변경한다.
4999와 5003에 해당하며 4999보다 작은 소수인 4993으로 변경한다는 의미입니다.
② 두 소수의 합이 정답보다 작을 경우 -> 더 큰 소수로 변경한다.
4993 + 5003 = 9996입니다. 따라서 5003을 5009로 크게 변경합니다.
위의 두 규칙을 꾸준히 진행하다 보면 결국에는 4919와 5081에서 결과를 얻을 수 있게 됩니다.
Python3 소스코드
# 백준 9020
import math
# 소수인지 판별하는 함수
def checkValue(numValue):
for comp in range(2, int(math.sqrt(number))+1):
if numValue % comp == 0:
return False
return True
# 차이가 가장 작은 두 소수 구하는 함수
def findValue(testCase, number):
# 중앙값을 기준으로 작은 소수와 큰 소수 찾기 (10일 경우 5를 기준 3과 7)
lowValue = max(N for N in prime_number if N < number)
highValue = min(N for N in prime_number if N > number)
while(1):
if lowValue + highValue == testCase:
print("%d %d" % (lowValue, highValue))
break
elif lowValue + highValue > testCase:
lowValue = max(N for N in prime_number if N < lowValue)
elif lowValue + highValue < testCase:
highValue = min(N for N in prime_number if N > highValue)
prime_number = list()
# 마지막 수인 10000의 두 소수는 4919, 5081
for number in range(2, 6000):
if checkValue(number):
# 소수이면 리스트에 저장
prime_number.append(number)
caseCount = int(input()) # 테스트케이스 개수
for cnt in range(caseCount):
testCase = int(input()) # 테스트케이스 값
if 4 <= testCase <= 100000:
midValue = testCase//2
if midValue in prime_number:
print("%d %d" % (midValue, midValue))
else:
findValue(testCase, midValue)
-끝-
'작업 > Problem Solving' 카테고리의 다른 글
| 백준 3009(네 번째 점) 파이썬(python) 해결 (0) | 2020.12.26 |
|---|---|
| 백준 1085(직사각형에서 탈출) 파이썬(python) 해결 (0) | 2020.12.26 |
| 백준 4948(베르트랑 공준) 파이썬(python) 해결 (0) | 2020.12.25 |
| 백준 1978(소수 찾기) 파이썬(python) 해결 (0) | 2020.09.10 |
| 백준 10250(ACM 호텔) 파이썬(python) 해결 (0) | 2020.09.10 |




